ALU

INFO

In this article, we will construct an ALU step by step

1-bit ALU (AND-OR)

Here is a simple 1-bit ALU 1-bit ALU that can perform AND (operation 0), OR (operation 1)

Add ADD operation to the 1-bit ALU

We can add Addition (operation 2 (10)) to this ALU as follows:

32-bit ALU using array of 1-bit ALUs

A 32-bit ALU can be constructed by arraying 32 1-bit ALUs. (this organization is called ripple-carry)

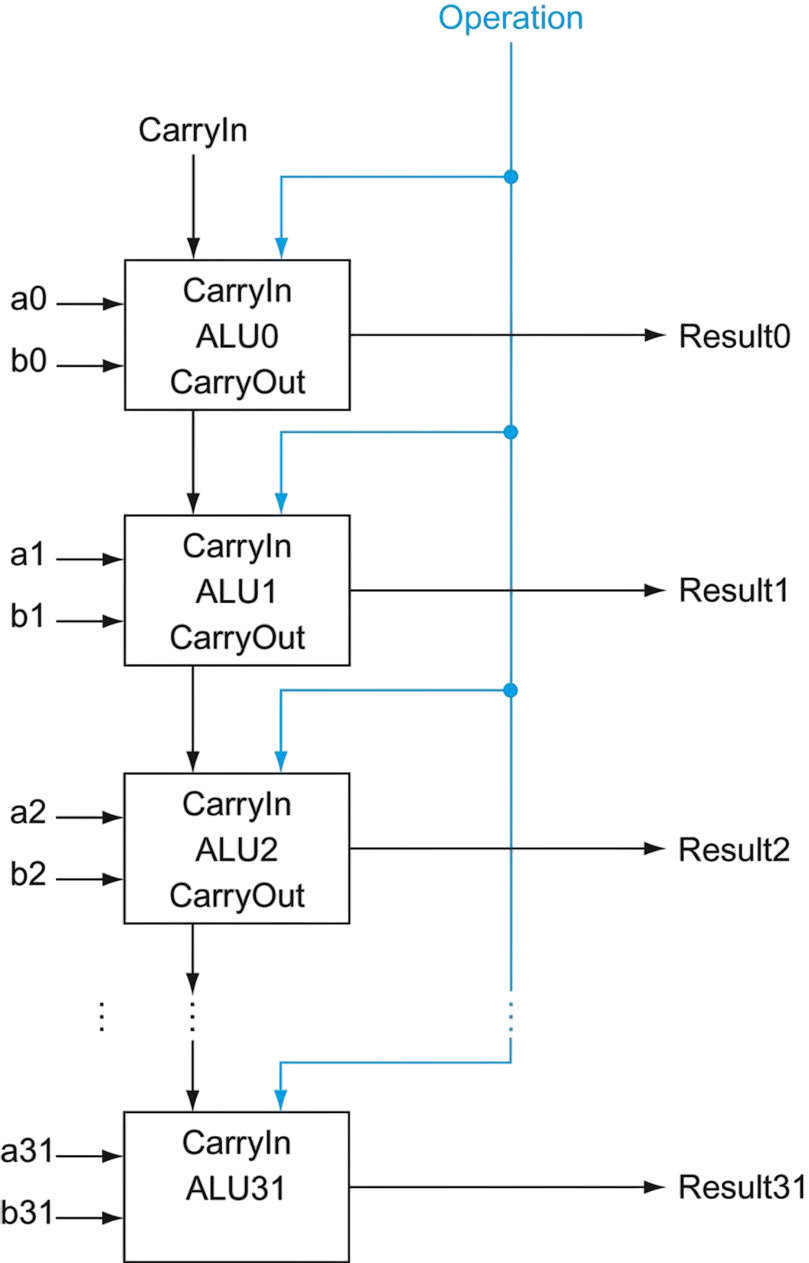
Subtraction using 2’s complement

Notice that the LSB still has a carry-in signal, even though it’s unnecessary for addition. However, if we set this carry-in to 1 instead of 0, the adder will then calculate $a+b+1$. By selecting the inverted of b, we get $a+\overline{b}+1=a+(\overline{b}+1)=a+(-b)=a-b$.

So for subtraction (a-b), we set both the carry-in and the Binvert to 1, and the operation to 2 (ADD).

NOR operation using AND and invert

NOR operation using AND and invert Instead of adding a separate NOR gate, we can add Ainvert to each 1-bit ALU and make use of the AND gate to perform NOR according to De Morgan’s law $\overline{A+B}=\overline{A}\cdot \overline{B}$.

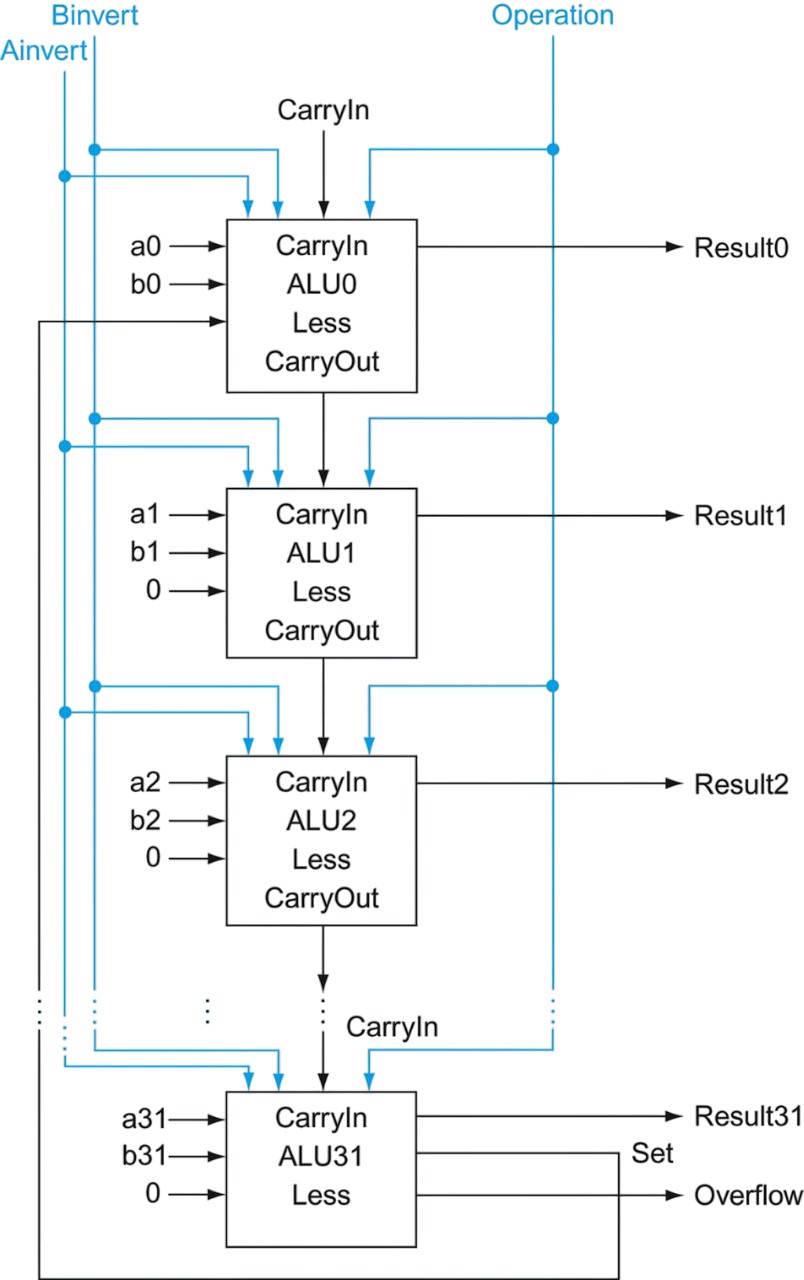
SLT

The Set Less Than (SLT) operation compares two numbers and sets the output to 1 if the first number is less than the second. Since $a<b⟺a-b<0$, we can use the subtraction operation to implement SLT. This can be done by comparing the MSB of the subtraction result.

• We will add a new input to the ALU called Less that will be connected to the mux which will also have a new operation (3) for SLT.
• In addition, we will add to the ALU of the MSB two outputs:
  • Set: which will capture the MSB of the 32-bit subtraction result. (if it is 1, then the result is negative). we will connect this output to the Less input of the LSB ALU.
  • Overflow: As long as we need a special ALU for the MSB, we added an Overflow output which detects overflow (in ADD or SUB operations). This is achieved by analyzing the carry into and out of the MSB.

The following figure shows the “general” 1-bit ALU with the new Less input.

The following figure shows the 1-bit ALU for the MSB:

And this is the 32-bit ALU constructed from 31 copies of the “general” 1-bit ALU and one copy of the MSB 1-bit ALU.

Notice that for subtraction, we need to set boththe carry-in and the Binvert to 1, while for addition or logical operations, we want both control lines (Carry-in and Binvert) to be 0. We can therefore simplify combining these two into a single control line called Bnegate. (or Binvert where it includes also the carry-in signal)

Final 32-bit ALU: Adding Zero detection for Equality check

• Equality of two numbers $a$ and $b$ can be determined by checking if $a-b=0$. (since $a=b⟺a-b=0$).
• Zero detection is done by checking if all bits are zero. So we can add OR gate to combine all the bits of the result and then invert the output using a NOT gate, to get the new Zero output of the ALU.
  • $\text{Zero}=\overline{{\text{Result}}_0+{\text{Result}}_1+\dots +{\text{Result}}_{31}}$

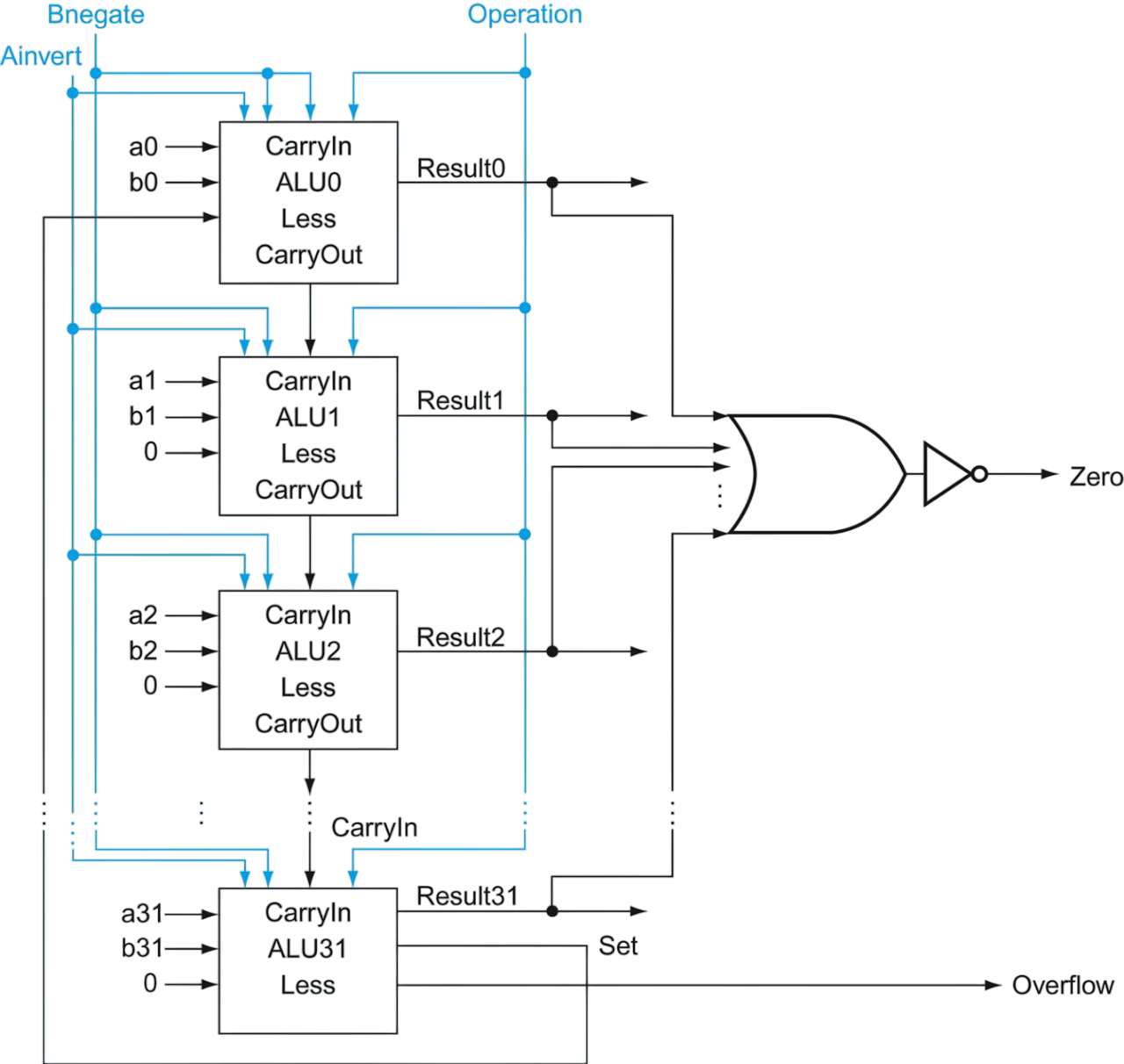
Table: The values of the three ALU control lines, Bnegate, and Operation, and the corresponding ALU operations.

ALU: Summary

Function	Ainv.	Binv.	Op.	Control	Dec	Output
AND	0	0	00	0000	0	Result = A AND B
OR	0	0	01	0001	1	Result = A OR B
add	0	0	10	0010	2	Result=A+B,
subtract	0	1	10	0110	6	Result=A-B,
slt	0	1	11	0111	7	Result0 = 1 if A < B, else 0
NOR	1	1	00	1100	12	Result = A NOR B
Here is a summary of the final 32-bit ALU:

Inputs

• $A$ and $B$ are the two 32-bit operands.
• $\text{ALU Operation}$ is a 4-bit control line that selects the operation to be performed.
  • 1 bit for Ainvert
  • 1 bit for Binvert (Bnegate)
  • 2 bits for the operation.
    • 00 AND
    • 01 OR
    • 10 ADD
    • 11 SLT

Outputs

• Result is the 32-bit output.
  • Result31 (or Sign (S)) is the MSB of the result (sign bit)
• Zero (Z) is 1 if all bits of Result are 0.
• Overflow (O) is 1 if signed overflow occurs (relevant only for addition and subtraction)
  • $\text{Overflow}={\text{CarryIn}}_{31}\oplus {\text{CarryOut}}_{31}$\
  • $\text{Overflow}=(a_{31}=b_{31})\wedge (a_{31}\ne {\text{Result}}_{31})$
  • addu ignores overflow while add raises an exception
    • Example:
      • a = b = 01000000 00000000 00000000 00000001 = 2^31 + 1 = 2,147,483,649
      • 01000000 00000000 00000000 00000001 (a)
      • + 01000000 00000000 00000000 00000001 (b)
      • = 10000000 00000000 00000000 00000010
      • so add will raise an exception because the sign bit of the result (1) is different from the sign bit of the operands (0)
• CarryOut (C) (which is actually the ${\text{CarryOut}}_{31}$ of the MSB) indicates overflow in overflow in unsigned addition or subtraction.

Timing

• Logical operations AND, OR, NOR, and NAND are executed simultaneously on all bits, with no dependency between bits. (Therefore these are called bitwise operations). The time required for these operations is constant, regardless of the number of bits (one or multiple).
• Arithmetic operations, such as ADD, SUB, and SLT (set less than), are sequential. As seen in the adder/subtractor circuit, these operations propagate from the least significant bit (right) to the most significant bit (left). The computation time is linearly dependent on the number of bits in the ALU.
  • The SLT operation takes the longest because, in addition to performing subtraction, it also calculates the set value and transfers it to the least significant bit (LSB) as feedback.
• The ALU is essentially a combinational logic circuit that performs all the described operations. The computation time of the ALU equals the time required for the longest operation. In the basic ALU described here, the longest operation is SLT.