MMN 11

עדיאל בן משה 208969378 אלגוריתמים 25א ממן 11

---

Q1

טענה א נכונה. נניח בשלילה שהעומקים שונים. אז קיים צומת v ב T2 בעומק d כך ש d גדול מהעומק של T1 וקטן מהעומק של T2. אבל עץ BFS מוצא את המסלול הקצר ביותר ל v. ולא יתכן שיהיו שני מסלולים קצרים ביותר בשני אורכים שונים.

דוגמה נגדית לטענה B

---

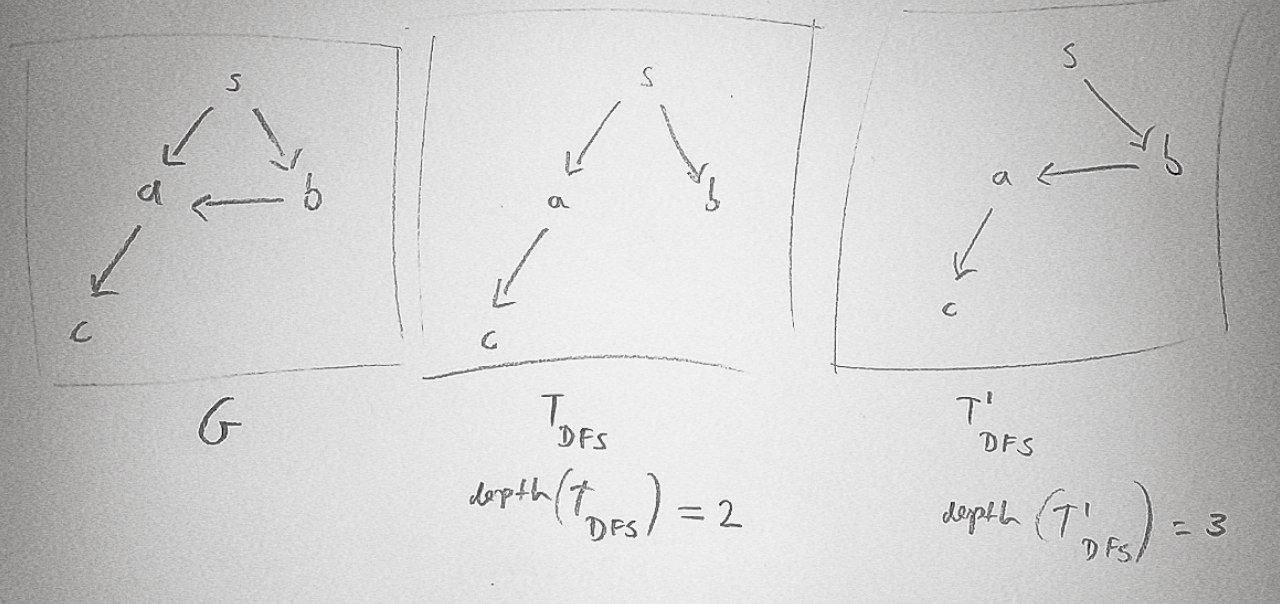
Q2

בהרצה 1 ו-3 כמו שרואים יוצא עץ אחד. בשנייה, שני עצים. כלומר אחד של Z ואחד של כל השאר.

---

---

Q3

input: graph G = (V, E), nodes U ⊆ V, start node s ∈ V, target node t ∈ V        
output: determine if a path exists from s to t in G satisfying our 2 conditions
run time: O(|V| + |E|) 
-------
G' = (V', E')
∀ v ∈ V: 
	V' = V' ∪ {v_1, v_2, v_3}

∀ (v,w) ∈ E: 
	if w not in U:
		∀ i ∈ {1,2,3}, E' = E' ∪ {(v_i, w_i)} 
	else:
		E' = E' ∪ {(v_1, w_2), (v_2, w_3)}

run BFS(G', s_1) to find the shortest path to t_3, which is in the form: (s_1, v_1, ... , u_2, v_2, ... , u_3, v_3, ... , t_3)

replace each v_i with v in the G and return the path